[알고리즘] 최소 신장 트리, 크루스칼 알고리즘(Kruskal Algorithm)
글의 요약 설명 부분. 150자를 적어주세요. 글의 요약 설명 부분. 150자를 적어주세요. 글의 요약 설명 부분. 150자를 적어주세요. 글의 요약 설명 부분. 150자를 적어주세요. 글의 요약 설명 부분. 150자를 적어주세요. 글의 요약 설명 부분. 150자입니다
목차
인프런 Rookiss님의 '자료구조와 알고리즘' 강의를 기반으로 정리한 필기입니다.
😎 [C++과 언리얼로 만드는 MMORPG 게임 개발 시리즈] Part3: 자료구조와 알고리즘 강의 들으러 가기!
최소 신장 트리 (Minimum Spanning Tree)
그래프는 정점과 간선으로 이루어진 자료구조이다. 간선은 정점과 정점의 인접 관계를 설명한다. 간석에 '가중치(Weight)'이라는 속성을 부여하면 그래프의 정점 간의 이동 비용을 계산할 수 있다.
최소 신장 트리(Minimum Spanning Tree)
간선의 수를 최소화해서, 모든 정점을 연결하는 방식. 예를 들어 통신 네크워크 구축한다면 '구축 비용', '전송 시간' 등을 최소로 해야 한다.
스패닝 트리의 특징
- N개의 정점을 N-1개의 간선으로 연결한다.
- 사이클을 포함하면 안 된다.
크루스칼 알고리즘(Kruskal Algorithm)
탐욕적인(greedy) 방법을 이용한다. 지금 이 순간에 최적인 답을 선택하여 결과를 도출한다.
상호 배타적 집합(Disjoint Set)을 이용한다.
크루스칼 알고리즘 생성 순서
- 그래프 내의 모든 간선을 가중치의 오름차순으로 정렬한다.
- 간선을 최소 신장 트리에 추가한다. 단, 새로 추가하는 간선으로 최소 신장 트리 내에 사이클이 형성되면 안 된다.

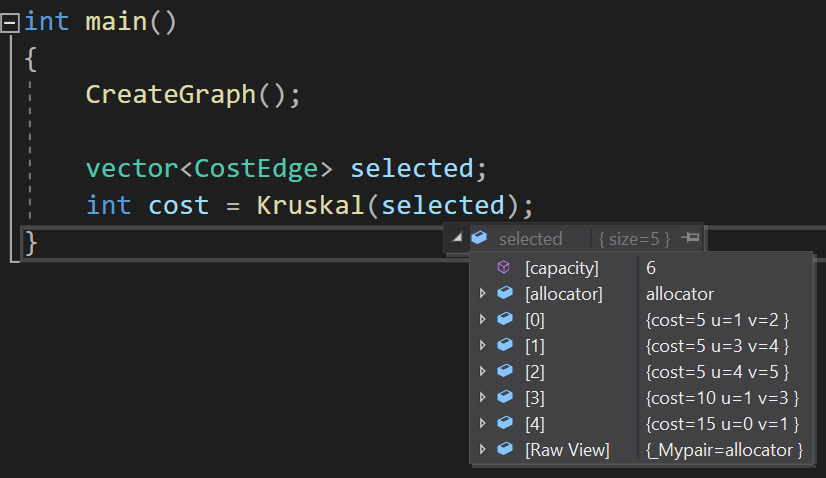
다음은 위의 그래프를 크루스칼 알고리즘으로 구현한 코드이다.
|
struct Vertex
{
// int data;
};
vector<Vertex> vertices;
vector<vector<int>> adjacent; // 인접 행렬
void CreateGraph()
{
vertices.resize(6);
adjacent = vector<vector<int>>(6, vector<int>(6, -1));
adjacent[0][1] = adjacent[1][0] = 15;
adjacent[0][3] = adjacent[3][0] = 35;
adjacent[1][2] = adjacent[2][1] = 5;
adjacent[1][3] = adjacent[3][1] = 10;
adjacent[3][4] = adjacent[4][3] = 5;
adjacent[3][5] = adjacent[5][3] = 10;
adjacent[5][4] = adjacent[4][5] = 5;
}
struct CostEdge
{
int cost;
int u;
int v;
bool operator<(CostEdge& other)
{
return cost < other.cost;
}
};
int Kruskal(vector<CostEdge>& selected)
{
int ret = 0;
selected.clear();
vector<CostEdge> edges;
for (int u = 0; u < adjacent.size(); u++)
{
for (int v = 0; v < adjacent[u].size(); v++)
{
int cost = adjacent[u][v];
if (cost == -1)
continue;
edges.push_back(CostEdge{ cost, u, v });
}
}
std::sort(edges.begin(), edges.end());
DisjointSet sets(vertices.size());
for (CostEdge& edge : edges)
{
// 같은 그룹이면 스킵 (안 그러면 사이클 발생)
if (sets.Find(edge.u) == sets.Find(edge.v))
continue;
// 두 그룹을 합친다
sets.Merge(edge.u, edge.v);
selected.push_back(edge);
ret += edge.cost;
}
return ret;
}
|
cs |
프림 알고리즘 (Prim's Algorithm)
그래프에서 최소 신장 트리를 만들어내는 알고리즘이다.
프림 알고리즘 생성 과정
- 노드가 하나도 없는 최소 신장 트리를 준비한다.
- 그래프에서 임의의 정점을 시작 정점으로 선택한 후 최소 신장 트리의 뿌리 노드로 삽입한다.
- 간선의 가중치를 조사한다. 가중치가 작은 간선들을 골라 이 간선에 연결된 인접 정점을 최소 신장 트리에 삽입한다. 새로 삽입되는 정점은 기존 노드와 사이클을 형성하면 안 된다.
- 최소 신장 트리가 그래프의 모든 정점을 연결할 때까지 3번 과정을 반복한다.
전체코드
Kruskal Algorithm 전체 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
|
#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <queue>
using namespace std;
class DisjointSet
{
public:
DisjointSet(int n) : _parent(n), _rank(n, 1)
{
for (int i = 0; i < n; i++)
_parent[i] = i;
}
// 니 대장이 누구니?
int Find(int u) // u는 최상위 노드
{
if (u == _parent[u])
return u;
return _parent[u] = Find(_parent[u]);
}
// u와 v를 합친다
void Merge(int u, int v)
{
u = Find(u);
v = Find(v);
if (u == v)
return;
if (_rank[u] > _rank[v])
swap(u, v);
// rank[u] <= rank[v] 보장됨
_parent[u] = v;
if (_rank[u] == _rank[v])
_rank[v]++;
}
private:
vector<int> _parent;
vector<int> _rank;
};
struct Vertex
{
// int data;
};
vector<Vertex> vertices;
vector<vector<int>> adjacent; // 인접 행렬
void CreateGraph()
{
vertices.resize(6);
adjacent = vector<vector<int>>(6, vector<int>(6, -1));
adjacent[0][1] = adjacent[1][0] = 15;
adjacent[0][3] = adjacent[3][0] = 35;
adjacent[1][2] = adjacent[2][1] = 5;
adjacent[1][3] = adjacent[3][1] = 10;
adjacent[3][4] = adjacent[4][3] = 5;
adjacent[3][5] = adjacent[5][3] = 10;
adjacent[5][4] = adjacent[4][5] = 5;
}
struct CostEdge
{
int cost;
int u;
int v;
bool operator<(CostEdge& other)
{
return cost < other.cost;
}
};
int Kruskal(vector<CostEdge>& selected)
{
int ret = 0;
selected.clear();
vector<CostEdge> edges;
for (int u = 0; u < adjacent.size(); u++)
{
for (int v = 0; v < adjacent[u].size(); v++)
{
int cost = adjacent[u][v];
if (cost == -1)
continue;
edges.push_back(CostEdge{ cost, u, v });
}
}
std::sort(edges.begin(), edges.end());
DisjointSet sets(vertices.size());
for (CostEdge& edge : edges)
{
// 같은 그룹이면 스킵 (안 그러면 사이클 발생)
if (sets.Find(edge.u) == sets.Find(edge.v))
continue;
// 두 그룹을 합친다
sets.Merge(edge.u, edge.v);
selected.push_back(edge);
ret += edge.cost;
}
return ret;
}
int main()
{
CreateGraph();
vector<CostEdge> selected;
int cost = Kruskal(selected);
}
|
cs |
코딩테스트 예시문제
78번
2023.04.26 - [코딩테스트/100문제] - [코딩테스트] 76~80번 그래프, DFS, BFS 관련 보충문제
[코딩테스트] 76~80번 그래프, DFS, BFS 관련 보충문제
<--! 드래그 방지 --> <--! 드래그 방지 --> 이 영역을 누르면 첫 페이지로 이동
designerd.tistory.com
'⭐ Programming > 자료구조와 알고리즘' 카테고리의 다른 글
| [알고리즘] 프림 알고리즘(Prim Algorithm)을 이용한 길찾기 (0) | 2022.11.08 |
|---|---|
| [알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)을 이용한 길찾기 (0) | 2022.11.07 |
| [알고리즘] 상호 배타적 집합(Disjoint Set) (1) | 2022.11.06 |
| [알고리즘] 해시 테이블 (Hash Table) (0) | 2022.11.06 |
| [알고리즘] 퀵 정렬 (Quick Sort) (0) | 2022.11.05 |
댓글
이 글 공유하기
다른 글
-
[알고리즘] 프림 알고리즘(Prim Algorithm)을 이용한 길찾기
[알고리즘] 프림 알고리즘(Prim Algorithm)을 이용한 길찾기
2022.11.08 -
[알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)을 이용한 길찾기
[알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)을 이용한 길찾기
2022.11.07 -
[알고리즘] 상호 배타적 집합(Disjoint Set)
[알고리즘] 상호 배타적 집합(Disjoint Set)
2022.11.06 -
[알고리즘] 해시 테이블 (Hash Table)
[알고리즘] 해시 테이블 (Hash Table)
2022.11.06
댓글을 사용할 수 없습니다.