[알고리즘] 정렬 Sorting
글의 요약 설명 부분.
SORTING 정렬
정렬(Sorting)이란 정해진 기준에 맞춰 데이터를 정리하는 알고리즘이다. 가장 흔한 예로 오름차순/내림차순 정렬이 있다.
정렬의 궁극적인 목적은 데이터를 빠르고 쉽게 찾을 수 있는 '탐색'에 있다.
|
1
2
3
4
5
6
7
8
9
10
|
int main()
{
vector<int> v{ 1, 5, 3, 4, 2 };
std::sort(v.begin(), v.end());
BubbleSort(v);
SelectionSort(v);
InsertionSort(v);
}
|
cs |
다음은 아래의 버블, 선택, 삽입 정렬이 공통적으로 사용하는 메인 함수다.
더보기
int main() { vector<int> v{ 1, 5, 3, 4, 2 }; std::sort(v.begin(), v.end()); BubbleSort(v); SelectionSort(v); InsertionSort(v); }
버블 정렬(Bubble Sort)
- (N-1) + (N-2) + ... + 3 + 2 + 1
- 등차수열의 합 = N * (N-1) / 2
- 0(N^2) 시간복잡도
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
void BubbleSort(vector<int>& v)
{
const int n = (int)v.size();
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < (n - 1 - i); j++)
{
if (v[j] > v[j + 1])
{
int temp = v[j];
v[j] = v[j + 1];
v[j + 1] = temp;
}
}
}
}
|
cs |
더보기
void BubbleSort(vector<int>& v) { const int n = (int)v.size(); for (int i = 0; i < n - 1; i++) { for (int j = 0; j < (n - 1 - i); j++) { if (v[j] > v[j + 1]) { int temp = v[j]; v[j] = v[j + 1]; v[j + 1] = temp; } } } }
선택 정렬(Selection Sort)
- (N-1) + (N-2) + ... + 3 + 2 + 1
- 등차수열의 합 = N * (N-1) / 2
- 0(N^2) 시간복잡도
// [3][J][5][K][9]
// [3][5][9][J][K]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
void SelectionSort(vector<int>& v)
{
const int n = (int)v.size();
for (int i = 0; i < n - 1; i++)
{
int bestIdx = i;
for (int j = i + 1; j < n; j++)
{
if (v[j] < v[bestIdx])
bestIdx = j; // 가장 작은값을 가지는 인덱스를 bestIdx로 만들어줌
}
// 교환
int temp = v[i];
v[i] = v[bestIdx];
v[bestIdx] = temp;
}
}
|
Insertion Sort 삽입 정렬
0(N^2) 시간복잡도
[5][J][9][3][K]
[5] [J][9][3][K]
[5][J] [9][3][K]
[5][9][J] [3][K]
[3][5][9][J] [K]
[3][5][9][J][K]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
void InsertionSort(vector<int>& v)
{
const int n = (int)v.size();
// 0(N^2) 시간복잡도
for (int i = 1; i < n; i++)
{
int insertData = v[i];
int j; // 삽입되어야 하는 데이터
for (j = i - 1; j >= 0; j--)
{
if (v[j] > insertData) // 이전 데이터와 비교하여 삽입되는 데이터가 더 크면
v[j + 1] = v[j]; // 이전 데이터 뒤에 위치해준다
else // 이전 데이터보다 작으면
break; // break로 빠져나간다.
}
v[j + 1] = insertData;
}
}
|
cs |
마무리
버블 < 선택 < 삽입 정렬순으로 더 효율적인 정렬 방식이다.
하지만 버블, 선택, 삽입 정렬 모두 시간복잡도가 N^2인 정렬 방식이다.
따라서 위의 3가지 정렬 방식은 지양해야 한다. 다른 게시물에 정리된 정렬 방식을 쓰는걸 권장한다.
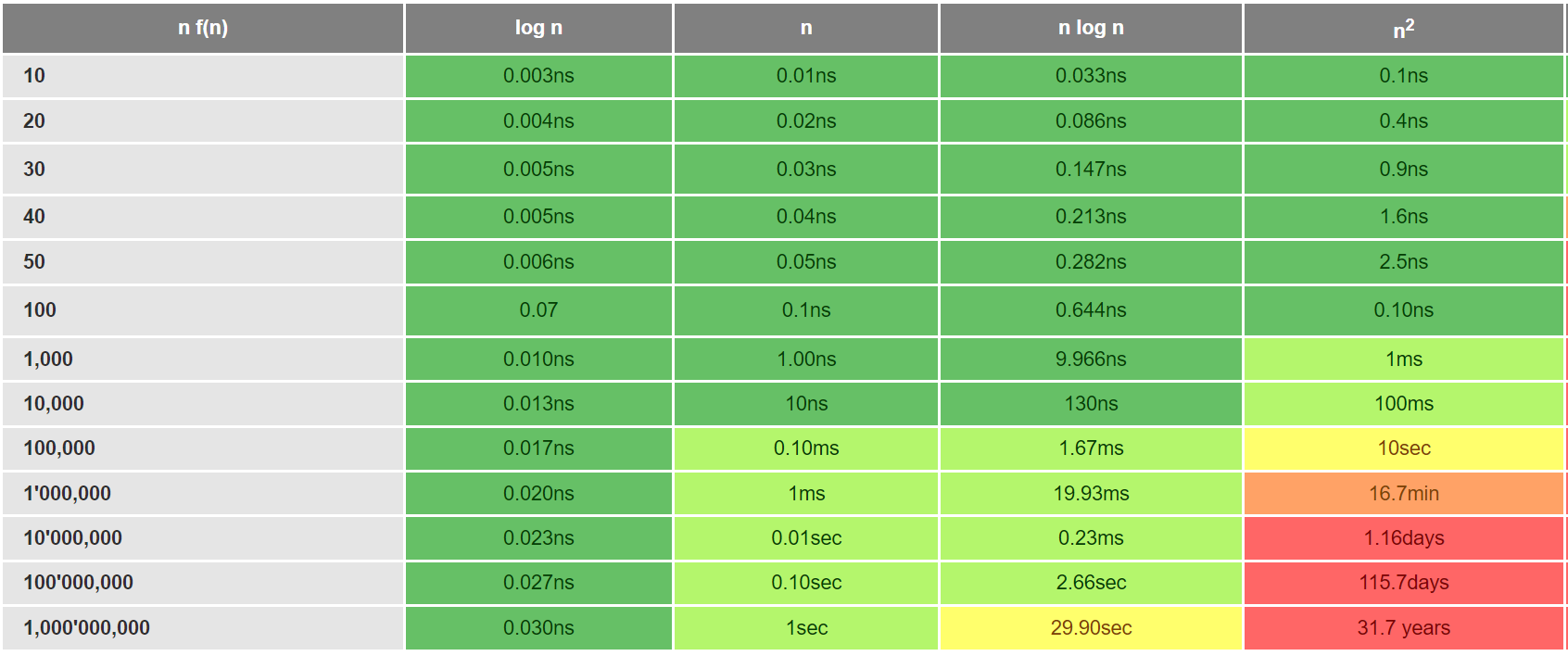
출처: https://cooervo.github.io/Algorithms-DataStructures-BigONotation/
Big O cheat sheets
About: I made this website as a fun project to help me understand better: algorithms, data structures and big O notation. And also to have some practice in: Java, JavaScript, CSS, HTML and Responsive Web Design (RWD). If you discover errors in the code or
cooervo.github.io
전체 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
|
#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <queue>
#include <thread>
using namespace std;
// C# 자료구조/알고리즘
// -> A* OpenList (PQ)
// -> C# List = C++ vector
// PQ O(logN)
// Red-Black Tree 0(logN)
// Sorting
// [3][J][5][K][9]
// [3][5][9][J][K]
// 1) 버블 정렬 (Bubble Sort)
void BubbleSort(vector<int>& v)
{
const int n = (int)v.size();
// (N-1) + (N-2) + ... + 3 + 2 + 1
// 등차수열의 합 = N * (N-1) / 2
// 0(N^2) 시간복잡도
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < (n - 1 - i); j++)
{
if (v[j] > v[j + 1])
{
int temp = v[j];
v[j] = v[j + 1];
v[j + 1] = temp;
}
}
}
}
// [3][J][5][K][9]
// [3][5][9][J][K]
// 2) 선택 정렬 (Selection Sort)
void SelectionSort(vector<int>& v)
{
const int n = (int)v.size();
// (N-1) + (N-2) + ... + 3 + 2 + 1
// 등차수열의 합 = N * (N-1) / 2
// 0(N^2) 시간복잡도
for (int i = 0; i < n - 1; i++)
{
int bestIdx = i;
for (int j = i + 1; j < n; j++)
{
if (v[j] < v[bestIdx])
bestIdx = j; // 가장 작은값을 가지는 인덱스를 bestIdx로 만들어줌
}
// 교환
int temp = v[i];
v[i] = v[bestIdx];
v[bestIdx] = temp;
}
}
// [5][J][9][3][K]
// [5] [J][9][3][K]
// [5][J] [9][3][K]
// [5][9][J] [3][K]
// [3][5][9][J] [K]
// [3][5][9][J][K]
// 3) 삽입 정렬 (Insertion Sort)
void InsertionSort(vector<int>& v)
{
const int n = (int)v.size();
// 0(N^2) 시간복잡도
for (int i = 1; i < n; i++)
{
int insertData = v[i];
int j; // 삽입되어야 하는 데이터
for (j = i - 1; j >= 0; j--)
{
if (v[j] > insertData) // 이전 데이터와 비교하여 삽입되는 데이터가 더 크면
v[j + 1] = v[j]; // 이전 데이터 뒤에 위치해준다
else // 이전 데이터보다 작으면
break; // break로 빠져나간다.
}
v[j + 1] = insertData;
}
}
int main()
{
vector<int> v{ 1, 5, 3, 4, 2 };
std::sort(v.begin(), v.end());
//BubbleSort(v);
//SelectionSort(v);
InsertionSort(v);
}
|
cs |
'⭐ Programming > 자료구조와 알고리즘' 카테고리의 다른 글
| [알고리즘] A* 길찾기 알고리즘 (0) | 2022.11.02 |
|---|---|
| [알고리즘] Heap Sort, Merging Sort 힙 정렬, 병합 정렬 (0) | 2022.11.01 |
| [알고리즘] 우선순위 큐 Priority Queue (0) | 2022.10.31 |
| [자료구조] 이진 트리, 힙 이론, 힙 트리 (0) | 2022.10.31 |
| [자료구조] 트리 기초 (0) | 2022.10.31 |
댓글을 사용할 수 없습니다.