[게임수학] 삼각함수

호도법(Radian 라디안)
각의 크기를 재는 SI 유도 단위이다. 호의 길이로 각도를 나타내는 방법이다. 기호는 rad 또는 c이며 이는 자주 생략된다. 어떤 각의 라디안 값은 같은 크기의 단위원 중심각이 대하는 호의 길이와 같다. '호의 길이 = 반지름 길이', '360도 = π = 180°
원 위의 점이 원점을 중심으로 반지름의 길이만큼 한 방향으로 움직였을 때 대응하는 각의 크기를 1 라디안(rad)이라고 정의한다. 이 때 원주만큼 움직였을때 대응하는 각의 크기는 2π 라디안(rad)이다.

부채꼴에서 육십분법으로 나타낸 중심각의 크기를 θ, 반지름의 길이를 r이라고 하면, 원둘레는 2πr이므로 호의 길이 l을 다음과 같이 나타낼 수 있다. l = 2πr * θ / 180
1°는 몇 라디안? 180/π
70°는 몇 라디안? 70 * 180/π
1 rad은 몇 도? π/180
1 rad ≈ 약 57.3°. 180/π ≈ 57.296°
2π = 360°, π = 180°, π/3 = 60°, π/4 = 45°, π/6 = 30°
Sin, Cos, Tan 항등식

Sin, Cos 그래프

Tan 그래프

역함수


코사인 법칙
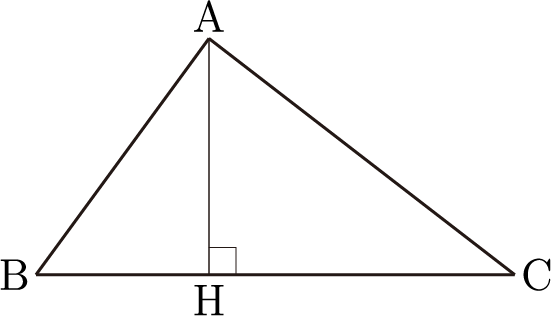
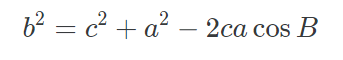
코사인 덧셈정리
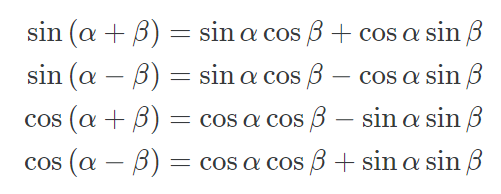
https://namu.wiki/w/%EC%82%BC%EA%B0%81%ED%95%A8%EC%88%98
삼각함수 - 나무위키
좌표평면 상 원점 O\rm OO가 중심인 단위원을 고려하자. 단위원 위의 한 점 P(x, y){\rm P}(x,\,y)P(x,y)에 대하여 xxx축의 양의 방향을 시초선[6]으로 잡는다. O\rm OO를 중심으로 시초선에서 반시계 방향
namu.wiki
'⭐ DirectX > 게임수학' 카테고리의 다른 글
| [게임수학] 왼손 좌표계 오른손 좌표계 (0) | 2022.05.25 |
|---|---|
| [게임수학] Matrix 행렬 (0) | 2022.05.22 |
| [게임수학] Vector (기하)벡터 (0) | 2022.05.21 |
댓글
이 글 공유하기
다른 글
-
[게임수학] 왼손 좌표계 오른손 좌표계
[게임수학] 왼손 좌표계 오른손 좌표계
2022.05.25 -
[게임수학] Matrix 행렬
[게임수학] Matrix 행렬
2022.05.22 -
[게임수학] Vector (기하)벡터
[게임수학] Vector (기하)벡터
2022.05.21
댓글을 사용할 수 없습니다.