[게임수학] Matrix 행렬

Matrix 행렬

 

 

행렬 곱셈

(앞 행렬의 행의 수) × (뒤 행렬의 열의 수)

즉, 앞 행렬이 m×n 크기이고 뒤 행렬이 n×r 크기인 경우 곱은 m×r 크기의 행렬이 된다.

행렬은 교환법칙 성립X, 결합법칙 성립O

 

 

 

 

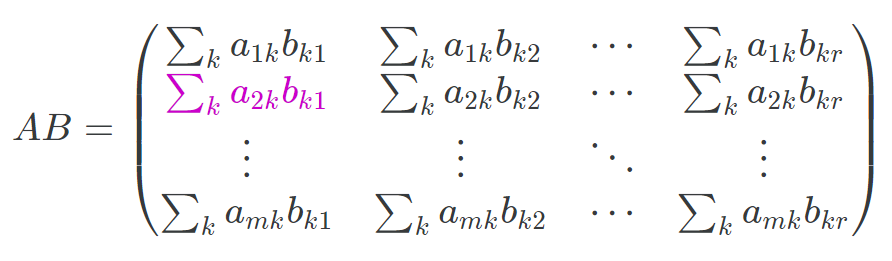
Digonal Matrix 대각 행렬

 

 

 

 

Unit Matrix(단위 행렬) 또는 Identity Matrix(항등 행렬)

 

\ 

 

Inverse Matrix 역행렬 

 

사각행렬 A의 곱셈에 대한 역원 A^-1을 말한다. A A^-1 = E(Identity Matrix) 

 

 

 

Transpose Matrix 전치행렬

 

행과 열을 뒤집은 행렬. 행렬 내의 원소를 대각선축을 기준으로 서로 위치를 바꾼 것을 말한다. 즉, m×n 행렬의 전치행렬은 n×m 행렬이 된다. 기호는  A^T로 나타낸다.

 

 

 

Orthogonal Matrix 직교행렬 

 

 직교행렬 x 전치행렬 = 단위행렬, 직교행렬의 전치행렬은 역행렬이다.

 

 

 

 

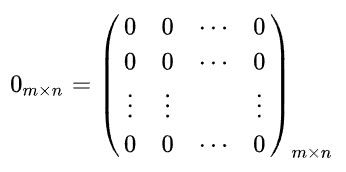
Zero Matrix 영행렬

 

모든 성분이 0인 행렬.

 

 

 

Transformation Matrix 행렬과 변환

 

 

Scaling Matrix 크기 변환 행렬

 

Rotation Matrix

 

Translation Matrix 

 

Reflection Matrix 

 

x축을 중심으로 θ만큼 회전 

 

y축을 중심으로 θ만큼 회전 

 

z축을 중심으로 θ만큼 회전 

 

 

 

 

 

 

https://namu.wiki/w/%EC%97%AD%ED%96%89%EB%A0%AC

역행렬 - 나무위키

 

https://namu.wiki/w/%EC%A0%84%EC%B9%98%ED%96%89%EB%A0%AC

전치행렬 - 나무위키