[게임수학] Vector (기하)벡터

 

Vector 벡터

 

크기와 방향 모두 가지고 있다. 벡터 사이의 '덧셈과 뺄셈'은 가능하나 '곱셈과 나눗셈'(내적, 외적, 직접곱은 엄밀히 말하면 곱셈이 아니다)은 불가능하다. 벡터와 스칼라의 곱셈 나눗셈은 가능하다.

 

벡터의 합연산

오브젝트의 이동에 사용한다. 

v1 + v2  ->  (v1.x + v2.x, v1.y + v2.y)

v1 -> rc

v2 -> 이동값

 

• 프레임 당 이동값
  • rc.pos += 이동값
• 초 당 이동값
  • rc.pos += 이동값 * delta
  • rc.pos += 단위벡터(방향) * 초당이동값(크기) * delta
  • 속도(velocity)

방향을 가지는 단위벡터를 구할 때 원의 반지름을(벡터의 크기 -> 스칼라) 1로 두면 

(벡터의 크기 x cosθ, 벡터의 크기 x sinθ) 으로 표현 할 수 있다.

 

 

결합법칙(Associative Law of Addition)

 

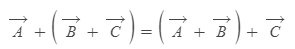
교환법칙(Commutative Law of Addition)

 

 

단위벡터 (Unit Vector)

 

길이가 1인 벡터. 

• 사용예시: 단위벡터에 스칼라(Scalar)값을 곱해줘서 원하는 방향으로 스칼라값만큼 이동시켜준다. 

 

 

 

영벡터 (Zero Vector 또는 Null Vector)

 

길이가 0인 벡터. 

• 사용예시: 벡터에 영 벡터를 곱해 해당 벡터를 0으로 만들 때 사용한다.

 

 

 

벡터의 정규화 (Normalization)

 

벡터를 벡터의 길이로 나누어 1로 만드는 것을 말한다. 벡터의 정규화 과정을 거쳐 방향만 남기게 한다.

본인 x ( 1 / 본인의 크기)

만약 벡터 v = ( 2, 3, -1)이라면 벡터의 정규화 과정은 다음과 같다.

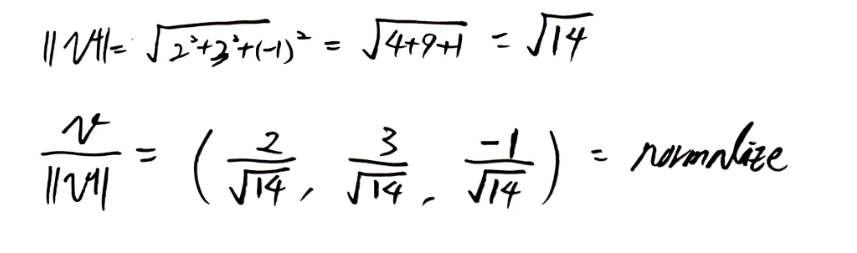
벡터의 정규화는 다음과 같은 상황에서 자주 사용한다.

• 방향이 같은 여러개의 벡터를 정규화해 같은 벡터로 통일시켜주고 싶을 때
• 벡터의 크기값을 없애고 방향값만 남겨주고 싶을 때
• 캐릭터 이동할 거리 = 정규화된 벡터값 x 스칼라값

 

 

벡터의 내적 (Inner Product 또는 Dot Product)

 

두 개의 벡터에 대한 내적은 두 개의 벡터가 이루는 각도를 구할 수 있다. 벡터의 내적을 구하면 스칼라가 나온다.

• 두 벡터의 내적 = 0, 두 벡터는 수직
• 두 벡터의 내적 > 0, 두 벡터의 내각은 예각(<90)
• 두 벡터의 내적 < 0, 두 벡터의 내각은 둔각(>90)

 

 

 

벡터의 외적 (Outer Product 또는 Cross Product)

 

두 개의 벡터에 대한 외적은 두 개의 벡터에 수직인 벡터를 구하는 연산이다. 벡터의 외적을 구하면 벡터가 나온다.

• 연산값은 크기와 방향을 모두 가지는 벡터값이다.
• 두 벡터의 외적 크기 = 두 벡터가 만들 수 있는 평행사변형 넓이와 같다
• 두 벡터의 외적 방향 = 오른나사 법칙(물리 자기장)을 따른다 
• 교환법칙 성립X
  • A x B = - (B x A)

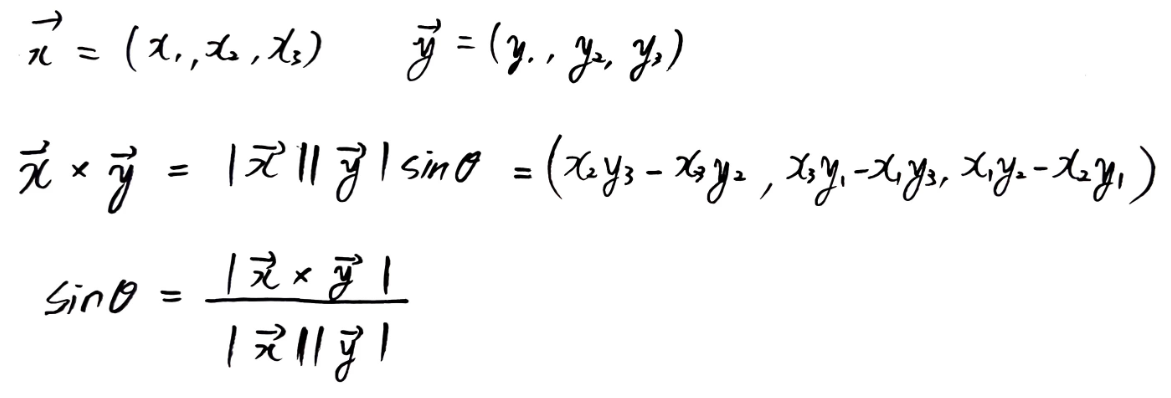
벡터의 외적은 다음과 같은 상황에서 사용된다.

• 법선을 구할 때. 두 벡터와 수직인 제 3의 벡터를 구할 때 사용.
• 삼각형의 넓이, 평행사변형의 높이와 넓이 구할 때
• 위치 좌우 판별 시 : '플레이어 시선 벡터 x UP 벡터'  두 개의 벡터를 외적하면 플레이어 기준 왼쪽에 있는 object는 양수, 오른쪽에 있는 object는 음수로 반환한다.
• 충돌 판정, 쿨타임 표시
• 선분교차(충돌) 판정의 경우 외적을 통한 CCW(Counter Clockwise) 알고리즘을 사용한다.

 

 

 

위의 내용들은 기하벡터이다. 코드를 짤 때 기하벡터와 위치벡터를 같이 사용하게 된다. 이 때 혼동하지 않도록 주의하자. 

 

 

 

---

http://www.findmean.com/%ec%88%98%ed%95%99/%eb%b2%a1%ed%84%b0/%eb%b2%a1%ed%84%b0%ec%9d%98-%eb%82%b4%ec%a0%81/

벡터의 내적 – findmean

 

http://www.findmean.com/%EC%88%98%ED%95%99/%EB%B2%A1%ED%84%B0/%EB%B2%A1%ED%84%B0%EC%9D%98-%EC%99%B8%EC%A0%81/

벡터의 외적 – findmean

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=sallygarden_ee&logNo=221265467087 

벡터의 곱셈(내적과 외적)

 

https://thrillfighter.tistory.com/190

벡터의 개념과 벡터의 내적,외적 - 게임 수학(3)